みなさんは、中学校数学で証明を学ばれたと思います。
この源流は、ユークリッド幾何学であります。起源数百年前、ユークリッドという人、若しくは、ユークリッドを中心とする学派の人々が、それまでの図形の性質を体系的にまとめ上げました。その書物の名前を、「ユークリッド原論」といいます。
ユークリッド原論は、演繹(えんえき)と呼ばれる思考法でまとめ上げられています。
かつて私が、20年前に滋賀大学大学院でお世話になった村上一三先生は、大学教員になる前、広島大学付属中高等学校で教鞭をふるっておられました。その頃、生徒から、「なぜ、数学を勉強しなければならないのか。」と問い詰められました。先生は、この問いに真摯に向き合い、その答えを導かれました。
その答えとは、この記事に載せる演繹的推論であります。
推論とは、予想の1つです。予想には、根拠のない憶測と根拠のある推測があります。推測の一種で、筋道だって考えられているものを推論と称しているのでしょう。そして、推論には、類比的推論(類推)、帰納的推論、演繹的推論の3つがあります。
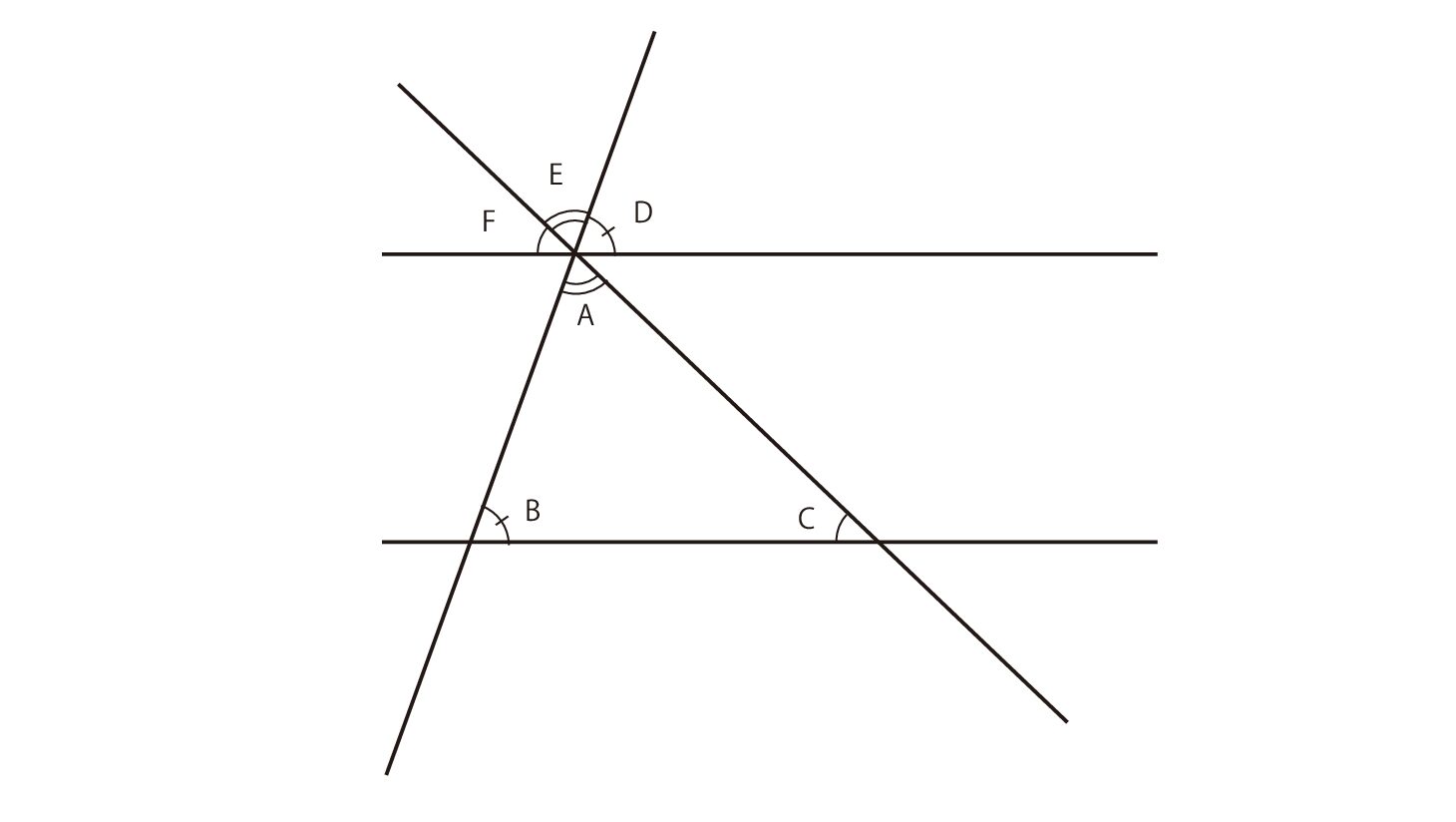
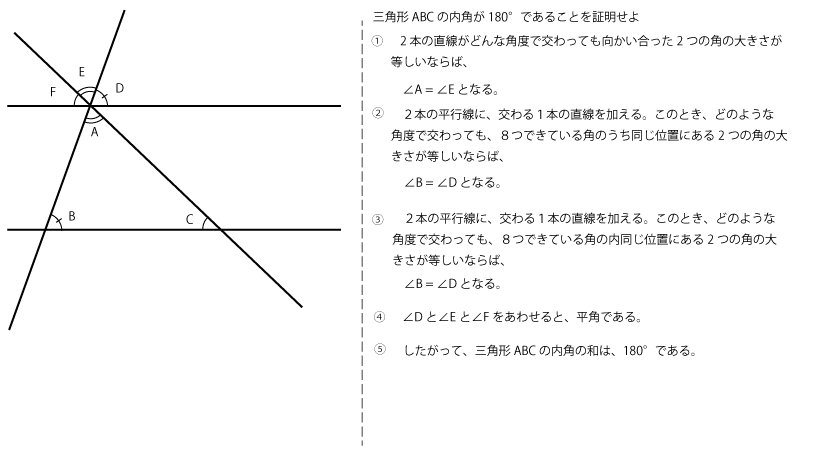
上の図とその横にある文字列を見てください。中学校の証明です。ただ、演繹を際出させるために、対頂角及び同位角という言葉をあえて使っていません。「〇〇ならば、△△となる。」という表現にしています。これは、〇〇という根拠が100%ただしければという条件付きの結論であります。ここでは、この結論を小さな結論と表現しておきましょう。これを、下のように「小さな結論」と「結論が導かれるための根拠」に分類し、表にしてみました。

どうですか。このようにして見ると、この証明は、3つの論から成り立っていることがわかります。この場合、①、②、③の論はそれぞれは、人類の経験上100%正しいです。したがって、三角形の内角は、180°になるわけです。
これは、数学の世界での話です。実生活では、このように行きません。しかしながら、人々は、あらゆる場面で予想して行動します。この予想を、①、②、③と分類し、検証することにより、どれだけ自らの予想が確かなのかを分析することができます。
長くなりましたので、その具体は、10月15日頃までにupいたします。